深度理解逻辑回归

引言

  所谓机器学习，听起来很高深莫测，实际上并不复杂，简单来说就是数据驱动的算法。而数据驱动就是指在给定的数据情况下，我们需要找到一种合适的算法对这些数据进行操作，从而实现我们预期的目标，具体我们需要做的任务就是找到合适的模型来描述输入到输出之间的映射关系，然后在使用优化的方法不断对模型中的参数进行优化，使得最后得到的结果鲁棒性最高。在上述的描述中，主要涉及两个方面：1.合适的模型 2.合适的优化算法。其实，我们在初中就接触过相关的领域，比如给定一系列坐标点（x，y），利用线性回归公式（最小二乘法）拟合曲线y=ax+b。其中，y=ax+b就是我们选择的模型，而最小二乘法就是对其参数a，b的优化算法。当然，这只是最简单的应用，实际机器学习的算法往往要比这个复杂很多，但究其本质还是一样的。
  对于机器学习而言，其功能非常强大，能完成分类、回归、转录、机器翻译、异常与检测、合成和采样等等。其中，分类与回归是机器学习的最基本的两项功能。上述举的例子就是回归算法。而今天，我主要介绍一种常用的分类算法——逻辑回归。对于分类的而言，逻辑回归是一种重要的学习方式，该方法所假设的函数在经过优化后的到模型适用性非常高。另外，之所以该方法在名称中带有回归二字，是因为其算法原理与线性回归之间有很深的联系，在下面介绍算法原理的时候我会重点讲解。

分类

  分类，顾名思义，就是将输入的数据分为不同的类别，其结果是离散的，比如预测明天的天气是去晴天还是非晴天。在计算机中，我们往往使用不同的数字代表不用的类别，比如1代表晴天，0代表非晴天。
  但是，如果算法仅仅只能够告诉我们分类的结果是非常不精准的，我们更期望算法能够告诉我们发生某种情况的概率，比如明天晴天的概率为80%，非晴天的概率为20%，这样的话我们的可操作性就会更强，可以人为的添加参数（优化）对算法进行矫正。仍以晴天为例，如果分类算法较为精准，我们可以用50%为阈值，如果晴天的概率大于50%，就是晴天；如果算法计算晴天概率比实际偏大，那我们可以设置60%为阈值，大于60%为晴天

线性回归

  在正式讲解逻辑回归的算法之间，首先我们需要了解一下线性回归的基本原理。我们假定输出y由输入x线性决定（这里的x,y都是向量)，其表达式为：

$$f(x)=\theta^{T} x······（1）$$

当输入变量只有一个时，就变成了我们熟悉的y=ax+b，此时，利用最小二乘法，具体的效果大致如下：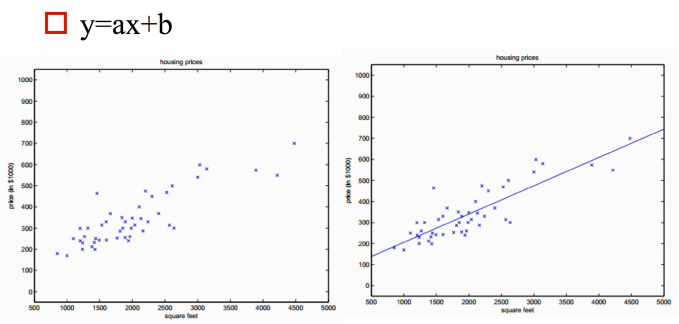

  当多个变量的时候，就由一维向量到多维，例如二维就会得到一个平面，而非一条直线了，其共同的特点就是模型是连续的，其值域为（-∞，+∞），这是线性回归模型的一个重要的特征。

逻辑回归

  逻辑回归是一种回归算法，该种算法主要应用于二分类的状况，例如明天北京是否会下雪，一个人五年内是否会得心脏病等等，由线性回归延伸出来的，那么具体是如何出现的呢？下面我来具体说明，仍以晴天为例：

1. 对于明天天气如何，我们该如何预测呢？首先，对于给定输入，比如温度，云层厚度，时间，风力，这些参数在算法中表现为x1,x2,x3……，我们最容易想到的就是令预测概率p（x）为x的线性函数，这样就和线性回归一致了，其值域为（-∞，+∞），并不符合我们的要求（概率应该在0~1之间），因此我们需要对其进行改进，使其符合我们的要求；
2. 如果我们需要限制值域，在机器学习中最常用的就是ln函数，因此我们做一个简单的调整，令lnp(x)为x的线性函数，也就是说p（x）=exp(ax+b)，但是该函数无论正负，均只能在一个方向上约束值域，因此还需要改进；
3. 最后，对lnp作简单的调整，令其在两个方向都被约束，我们用的方法是逻辑转换，令ln(p/1-p)为x的线性函数，那么p（x）的值域就是[0,1]
     因此逻辑回归的表达式为（在印刷体中我们往往都采用log代表ln）： $$\log \frac{p(x)}{1-p(x)}=\beta_{0}+x \beta··········（2）$$

如（2）中所示，p（x）为事情发生的概率，令$\log \frac{p(x)}{1-p(x)}$成为x的线性函数，解得p(x)为：

$$\mathrm{p}\left(x ; \beta_{0}, \beta\right)=\frac{1}{1+e^{-\left(\beta_{0}+x \beta\right)}}··········（3）$$

（3）式相比于（2）式更容易理解条件概率p（x），但（2）式更能凸显逻辑回归与线性回归之间的关系。
如图所示：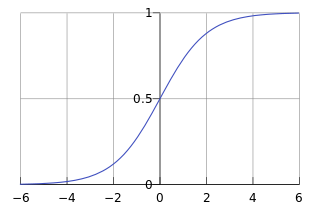

该图为函数逻辑回归曲线的大致形状，基本完成了我们期望的条件：曲线较为平滑，值域位于[0,1]。

主要特征

1. 一般取$\beta_{0}+x \quad \beta=0$为分类的边界，那么如果x是一维，那么分类边界就是一个点（类似在数轴上分类）；如果是二维分类边界就是一条直线，以此类推。之所以如此设置，是因为设置β0+ x β= 0为边界后，我们可以认为当算法输出的概率p（x）≥0.5时，分类结果 Y为1,；当p<0.5时，分类结果Y为0。或者说算法输入的$\beta_{0}+x \quad \beta≥0$时，分类结果为1；$\beta_{0}+x \quad \beta<0$时，分类结果为0（目前只考虑二分类的情况，多种分类情况在后面有介绍）。这样我们就可以把前面计算得到的概率转换为分类的结果了，既得到了分类的条件概率，又得到了分类的结果。
2. 逻辑回归计算得到的条件概率是由数据点到边界之间的距离决定的，为$\frac{\beta_{0}+x \beta}{|\beta|}$。也就是说如果距离边界远，那么为1（或者0）的概率就会越大。另外这个公式也说明了当||β||越大时，在同一数据集下，分类得到的概率会更像极端（0,1）靠近，如下图所示
   
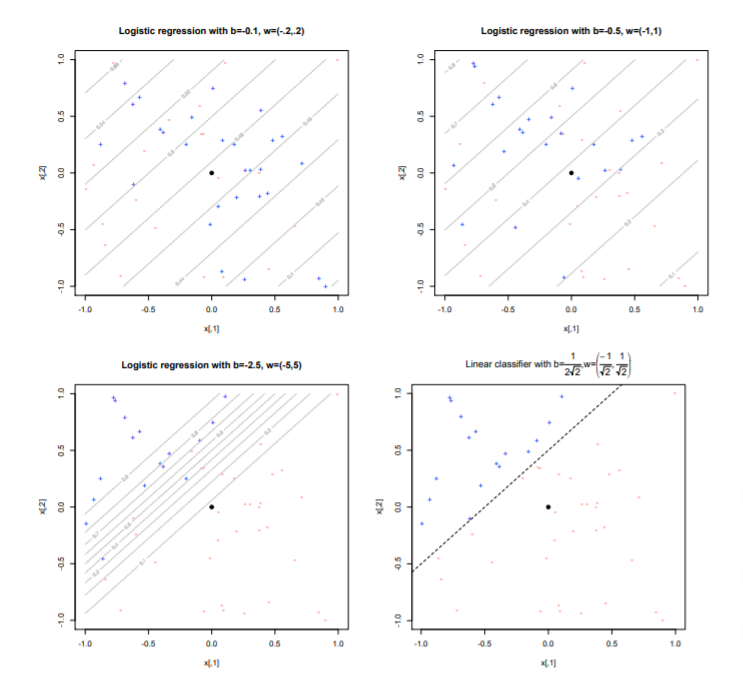
   （备注：最后一种是用线性分类的方式进行分类的）
3. 逻辑回归是跟据线性回归演化而来，提出时间早，科学家们对其研究较为透彻，运用较为熟练。此外，该算法较为简单，且适用性较强，机器学习的算法在准确度够得情况下，尽量选择较为简单的算法，避免出现过拟合

对于多分类的逻辑回归

逻辑回归本质上是对二分类的事件进行的分类，但是对于多分类的情况，我们可以通过建立多个分类模型，将多分类差分成多个二分类的情况，在利用逻辑回归进行分类，如图所示：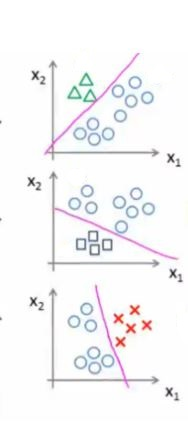

一般而言如果存在n中情况，我们会设置n个分类器，每个分类器对其中一种进行识别，其条件概率的计算公式为：

$$P(Y=c \mid X=x)=\frac{e^{\beta_{0}^{(c)}+x \beta^{(c)}}}{\sum_{i=1}^{n} e^{\beta_{0}^{(j)}+x \beta^{(i)}}}$$

判别方法与之前类似，如果超过0.5就认为是第c类。值得一提是，当只有两种情况时，令$\beta^{0}=\beta_{0}^{(1)}-\beta_{0}^{(0)}$以及$\beta=\beta^{(1)}-\beta^{(0)}$时，多情况的逻辑分类就转换成二分类的情况了。

下面是我自己的推导过程：