通俗理解奇异值分解

参考链接：

引言

机器算法的核心就是如何妥善的处理数据，但是当我们接触到一大堆原始杂乱的陌生数据时，往往会感到手足无措，因此我们需要对原始数据压缩，从而找到影响结果变化的主要因素与次要因素，奇异值分解就为我们提供了相应的方法，便于我们从茫茫的数据中找到关键因素，当然这种方法不仅仅局限于数据压缩，还有其他强大的功能，在此就不一一介绍了。

特征值分解

在正式接触奇异值分解之前，我们先来回顾在线性代数中学到的特征值分解(对角化)。首先特征值分解具有一定的局限性，只能应用于方阵，并且该方阵还要满足每个特征值对应的特征向量线性无关的最大个数等于该特征值的重数才能够对角化。对于n维可对角化的矩阵A可写成以下形式：

$A=V \Lambda V^{-1}$

具体表现形式为：

$A=\left[\begin{array}{} \mid & \mid & \mid \\ \mathbf{v}_{1} & \mathbf{v}_{2} & \mathbf{v}_{3} \\ \mid & \left.\right|& \mid \end{array}\right]\left[\begin{array}{} \left.\mid \begin{array}{} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]\left[\left.\begin{array}{} \mid & \mid & \mid \\ \mathbf{v}_{1} & \mathbf{v}_{2} & \mathbf{v}_{3}\\ \mid & \left.\right|& \mid \end{array}\right]^{-1}\right. \end{array}\right.$

上式中，v1,v2,v3为矩阵A的特征向量，一般情况下我们会把特征向量标准化，即满足|| V ||=1。然而，这种特征值分解只能应用于部分方阵。然而，在我们实际的数据中，大部分都并非方阵，因此我们需要对这种方法进行拓展，从而提出了奇异值分解，来应对普遍情况。

奇异值分解

$ A A^{T} $与$ A^{T} A $这两个矩阵对于奇异值分解来说是十分重要的两种矩阵，它们具有以下特征：

1.对于任意维度的矩阵A，都存在$ A A^{T} $与$ A^{T} A $；

2.实对称矩阵，特征向量正交；
3.方阵；
4.半正定；
5.两者具有相同的正数特征值，该特征值得算术平方根称之为奇异值
6.两者的秩相等，且与矩阵A相同。
这样的话，我们令$ u_{i} $为矩阵$ A A^{T} $的特征向量，令$ v_{i} $为矩阵$ A^{T} A $的特征向量,则我们称由$ u_{i} $，$ v_{i} $构成的矩阵$U$，$V$为矩阵A的奇异向量，具体表达式如下：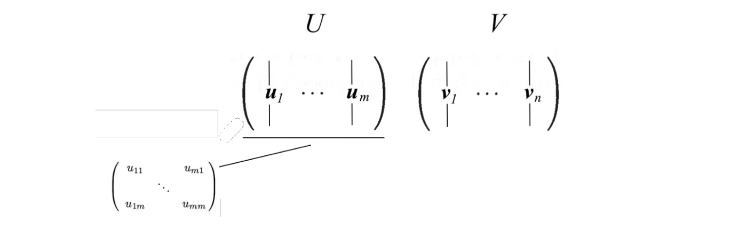

也就是说：

$\left(A^{T} A\right) v_{i}=\lambda_{i} v_{i}$ $\left(A A^{T}\right) u_{i}=\lambda_{i} u_{i}$

根据之前$ A A^{T} $与$ A^{T} A $的性质可知，我们可以通过正交分解使得$U,V$为正交矩阵。有了上述的基础概念，下面引入核心公式，奇异值分解认为，任意维度的矩阵A都可以被分解为以下形式：

$A=U S V^{T}$

其中，$U,V$就是矩阵A的奇异向量；S是对角阵，由奇异值构成。矩阵的排列顺序，一般按照奇异值从大到小排列，方便统一化管理和后续操作：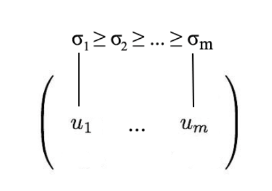

那么奇异值是如何计算的呢？

$A=U \Sigma V^{T} \Rightarrow A^{T}=V \Sigma U^{T} \Rightarrow A^{T} A=V \Sigma U^{T} U \Sigma V^{T}=V \Sigma^{2} V^{T}$

所以说奇异值矩阵等于特征值矩阵的算术平方根。相比于之前的特征值分解，SVD可以应用于任意维度的矩阵，并且U,V是正交矩阵，S是对角阵，具体应用的时候会非常的方便。

奇异值分解矩阵

为了让大家有一个深刻的印象，我举一个简单的例子来具体说明SVD是如何分解矩阵的。
对于矩阵A：

$A=\left(\begin{array}{ccc} 3 & 2 & 2 \\ 2 & 3 & -2 \end{array}\right)$

计算$ A A^{T} $与$ A^{T} A $的值得：

$A A^{T}=\left(\begin{array}{cc} 17 & 8 \\ 8 & 17 \end{array}\right), \quad A^{T} A=\left(\begin{array}{ccc} 13 & 12 & 2 \\ 12 & 13 & -2 \\ 2 & -2 & 8 \end{array}\right)$

上述矩阵都是半正定的，其特征值为25、9，也就是说A的奇异值为5、2。另外，这两个矩阵之间的联系为：

因此SVD的表达式为：

$A=U S V^{T}=\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ 1 / \sqrt{2} & -1 / \sqrt{2} \end{array}\right)\left(\begin{array}{ccc} 5 & 0 & 0 \\ 0 & 3 & 0 \end{array}\right)\left(\begin{array}{rrr} 1 / \sqrt{2} & 1 / \sqrt{2} & 0 \\ 1 / \sqrt{18} & -1 / \sqrt{18} & 4 / \sqrt{18} \\ 2 / 3 & -2 / 3 & -1 / 3 \end{array}\right)$

上述所说的只是基本应用，下面我对SVD的公式进行基本的变换：

$\begin{array}{l} A=U S V^{T} \\ A V=U S \end{array}$

也就是说SVD认为矩阵A是其所有奇异值与其对应的奇异向量的组合：

$A=\sigma_{1} u_{1} v_{1}^{T}+\ldots+\sigma_{r} u_{r} v_{r}^{T}$

上述公式是理解SVD矩阵分解的关键，它提供了一种重要的方法去拆解m*n数据矩阵至r个元素，现在我们在来重新分析下之前的例子是如何工作的：

$A=\left(\begin{array}{ccc} 3 & 2 & 2 \\ 2 & 3 & -2 \end{array}\right)$

矩阵A可以被拆解为：

$\begin{aligned} &=5\left(\begin{array}{ccc} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)\left(\begin{array}{cccc} 1 / \sqrt{2} & 1 / \sqrt{2} & 0 \end{array}\right)+3\left(\begin{array}{cc} 1 / \sqrt{2} \\ -1 / \sqrt{2} \end{array}\right)\left(\begin{array}{ccc} 1 / \sqrt{18} & -1 / \sqrt{18} & 4 / \sqrt{18} \end{array}\right)\\ &=\left(\begin{array}{ccc} 3 & 2 & 2 \\ 2 & 3 & -2 \end{array}\right) \end{aligned}$

奇异值分解应用

moore-penrose伪逆

对于线性方程组而言，我们往往需要计算矩阵的逆，如下图所示：

$\begin{aligned} A x &=b \\ x &=A^{-1} b \end{aligned}$

但是对于大部分矩阵而言，都没有办法求其逆矩阵，因此在求解方程组时需要逆矩阵的替代品，moore-penrose伪逆提供了这样的一种方法，可以计算矩阵A的伪逆值，使得$ \left|A A^{+}-I_{n}\right|_{2} $ 最小，也就是伪逆矩阵$A^{+}$的相关性质最接近其逆矩阵，因此线性方程组的解就可以被估计为：

$\begin{aligned} A x &=b \\ x & \approx A^{+} b \end{aligned}$

其中，为逆矩阵$A^{+}$的具体求解方式如下：

$\begin{array}{l} A x=b \\ (U, D, V) \leftarrow \operatorname{svd}(A) \\ A^{+}=V D^{+} U^{T} \\ x=A^{+} b \end{array}$

我们以一个简单的例子来具体说明：
$A=\left[\begin{array}{ll}1 & 1 \\ 1 & 1\end{array}\right] \quad$

$A=U \Sigma V^{T}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right]\left[\begin{array}{cc}2 & 0 \\ 0 & 0\end{array}\right] \frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right]$

$A^{+}=V \Sigma^{+} U^{T}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right]\left[\begin{array}{cc}1 / 2 & 0 \\ 0 & 0\end{array}\right] \frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right]=\frac{1}{4}\left[\begin{array}{cc}1 & 1 \\ 1 & 1\end{array}\right]$

moore-penrose伪逆的求解是基于奇异值分解的，通过上面的例子我们可以看出即便方阵不可逆，我们也能通过奇异值分解的方法得到其伪逆矩阵，也就是说该方法对于任意维度的任意矩阵都能适用。此外，待求矩阵A 的列数如果大于行数，得到就是所有可行解中L2范数最小的一个，如果相反，就是L2(Ax−y)最小

数据压缩

在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵:

$A_{m \times n}=U_{m \times m} \Sigma_{m \times n} V_{n \times n}^{T} \approx U_{m \times k} \Sigma_{k \times k} V_{k \times n}^{T}$

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵$U_{m \times k}, \sum_{k \times k}, V_{k \times n}^{T}$来表示,这样就可以以舍弃部分精度来减少数据量。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。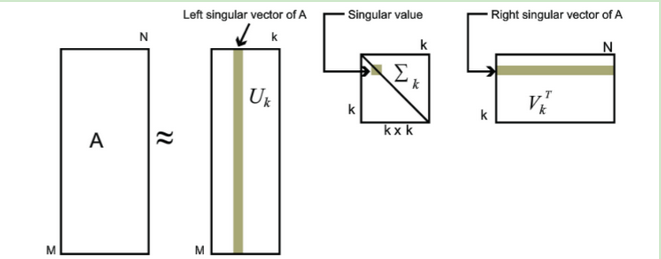

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪，PCA具体原理可以参考如何通俗易懂地讲解什么是 PCA 主成分分析。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。