通俗理解Seq2Seq模型+Attention机制(待修正)

seq2seq模型

seq2seq本质上是一种encoder-decoder的框架，最典型的应用就是机器翻译问题，模型先使用编码器对源语言进行编码，得到固定长度的编码向量，然后在对该编码向量进行解码，得到对应的翻译语言向量。因为输入和输出都是序列数据，因此又被称为sequence-to-sequence，简称seq2seq，目前应用最多的编码解码器是RNN(LSTM，GRU)，但编码解码器并不仅限于RNN。

传统的几种seq2seq方式

1.输入 $x$通过encoder编码，即RNN结构(这里以RNN结构为例，但不仅限于RNN结构)通过隐藏状态$h_{1}, h_{2}, \ldots, h_{t}$的不断传播，在传播过程中同时会产生输出 $y_{1}, y_{2}, \ldots, y_{t}$ ，然后形成编码向量 $\left[y_{1}, y_{2}, \ldots, y_{t}\right]$ ，在解码过程中编码向量每一步都会输入给decoder。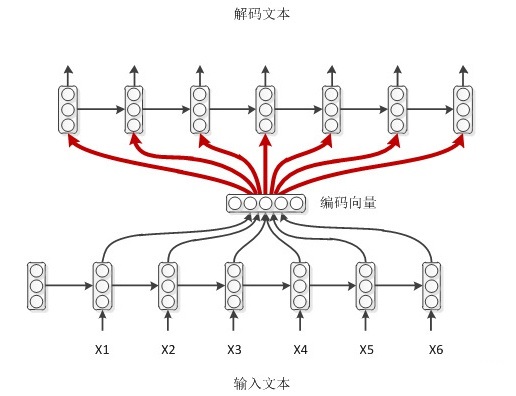

2.如果decoder同样也是个RNN结构的话，那么可以利用上一时刻的输出来帮助预测。encoder的编码赋值给了decoder的初始hidden。decoder的初始标签是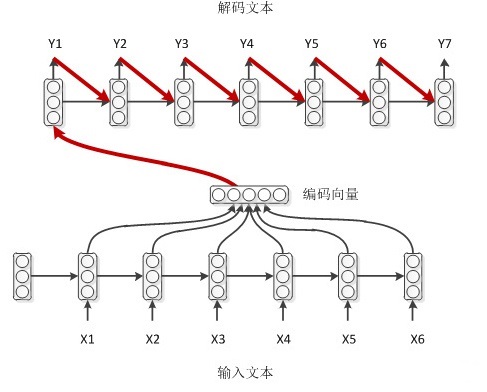特色的开始标签，对应着词表中这个标签的embedding。

3.结合了前两种模式，decoder每一时刻的输入不仅有来自encoder的编码向量，还有上一时刻的输出，同时还有上一时刻的hidden。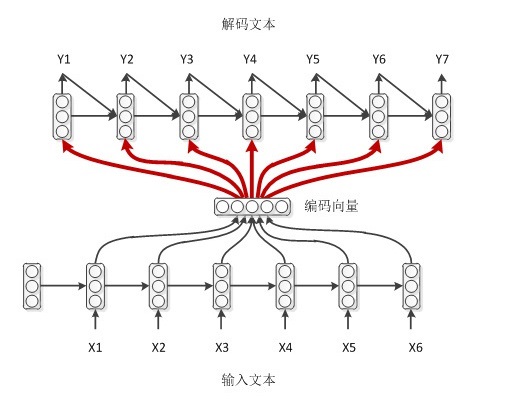

4.带有attention机制的编解码，encoder的RNN每一步都有一个输出 [公式] ，给每一个 [公式] 一个权重，计算带权求和的向量。这样做的好处是，每预测一个词都和原文本的部分最相关。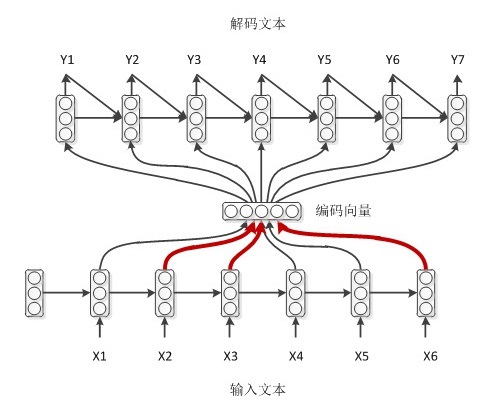

attention编解码的过程

输人： $\quad x=\left(x_{1}, \ldots, x_{T_{x}}\right),$ 输出： $\quad y=\left(y_{1}, \ldots, y_{T_{y}}\right)$
$h_{t}=R N N_{\text {encoder }}\left(x_{t}, h_{t-1}\right),$ Encoder方面接受每个单词的embedding以及上一个时 间点的hidden state, 输出是该时间点的hidden state。 $s_{t}=R N N_{\text {decoder}}\left(y_{t-1}^{\tilde{\tau}}, s_{t-1}\right),$ Decoder方面接受的是目标句子里单词的word
embedding以及上一个时间点的hidden state。在计算 $s_{1}$ 时, $\quad \tilde{y}_{0}$ 即encoder的编码向量, 可以是Encoder最后的hidden state, $\quad h_{t}$ 通过decoder的hidden states和encoder的hidden states来计算一个分数 $e_{i j}=\operatorname{score}\left(s_{i}, h_{j}\right)$
it算每一个encoder的hidden states的权重: $\quad \alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)}$
・ 最后得到context vector，是对于encoder输出的hidden states的一个加权平均 $c_{i}=\sum_{j=1}^{T_{x}} \alpha_{i j} h_{j}$

• 将context vector和decoder的hidden states串接起来 $\tilde{s}_{t}=\tanh \left(W_{c}\left[c_{t} ; s_{t}\right]\right)$
  ・计算最后的输出概率： $\quad p\left(y_{t} \mid y<t, x\right)=s o f t m a x\left(W_{s} \tilde{s}_{t}\right)$
  关于上式中的score方法：
  (1) dot score function: 输入是encoder的所有hidden states H: 大小为(hid dim,seq length)。decoder在一个时间点上的hidden state, s: 大小为(hid dim, 1)。
  ・ 旋转H为(seq length, hid dim)与s做点杰得到大小为(sequence length,
  1)的分数。
  ・ 对分数做softmax得到合为1的权重。 将H与上一步得到的权重做点乘得到大小为(hid dim, 1)的context vector。
  (2) General score function: 输入是encoder的所有hidden states H: 大小为(hid $\operatorname{dim}_{-} 1,$ seq length), decoder在一个时间点上的hidden state, s: 大小为(hid dim_2, 1), 此处两个hidden state的纬度不一致。
  旋转H为(seq length, hid dim1)与Wa(大小为hid dim_1,hid dim_2)做点乘，再和s做点乘得 到一个大小为(seq length, 1)的分数。
  ・ 对分数做softmax得到一个合为1的权重。 将H与第二步得到的权重做点拜得到一个大小为(hid dim_1, 1)的context vector。

attention机制的原理

神经学中的注意力机制有两种：

(1)自上而下的有意识的注意力，称为聚焦式注意力(Focus Attention)，聚焦式注意力是指有预定目的，依赖任务的，主动有意识地聚焦与某一对象的注意力。

(2)自下而上的无意识的注意力，称为基于显著性注意力(Saliency-Based Attention)。是由外界刺激驱动的注意，不需要主动去干预，和任务无关。如果一个对象的刺激信息不同于其周围信息，一种无意识的“赢者通吃”(Winner-Take-All)或者门控(Gating)机制就可以把注意力转向这个对象。

当你在听你的朋友说话时，你专注于你朋友的说话而忽略了周围其他的声音，这就是聚焦式注意力，当你在其他周围声音中听到了感兴趣的词时，你会马上注意到，这是显著性注意力。

给定N组信息输入 $X=\left[x_{1}, x_{2}, \ldots, x_{N}\right],$ 每个向量 $x_{i}, i \in[1, N]$ 都表示一组输入信 息。注意力机馳的计算分为两步：一是在所有输入信息上计算注意力分布, 二是根据注意力分布来 计算输入信息的加权平均。

注意力分布：为了从N个输入向量 $\left[x_{1}, x_{2}, \ldots, x_{N}\right]$ 中选择出和某个特定任务相关的信息, 需 要引入一个和任务相关的表示称为直询向量(Query Vector)，并通过一个打分函数score0计算每 个输入向量和直词向量之间的相关性。
给定一个和任务相关的直词向量q, 用注意力变量 $z \in[1, N]$ 来表示被选择信息的索引位置, 即 $z=i$ 表示选择了第i个输入向量。首先计算在给定q和X下，选择第i个输入向量的概率 $\alpha_{i}$ (权 重)

$$\alpha_{i}=p(z=i \mid X, q)=\operatorname{softmax}\left(s\left(x_{i}, q\right)\right)=\frac{\exp \left(s\left(x_{i}, q\right)\right)}{\sum_{j=1}^{N} \exp \left(s\left(x_{j}, q\right)\right)}$$

$\alpha_{i}$ 为注意力分布权重, $\quad s\left(x_{i}, q\right)$ 为注意力打分函数, 打分函数有很多种方式比如 :

1. 加性模型: $\quad s\left(x_{i}, q\right)=v^{T} \tanh \left(W x_{i}+U q\right)$
2. 点积模型： $\quad s\left(x_{i}, q\right)=x_{i}^{T} q$
3. 缩放点积模型: $\quad s\left(x_{i}, q\right)=\frac{x_{i}^{T} q}{\sqrt{d}}$
4. 双线性模型: $\quad s\left(x_{i}, q\right)=x_{i}^{T} W q$
   $W, U, v$ 为可学习的参数, $\quad d$ 为输入向量的维度。
   点积模型在实现上更好的利用了矩阵乘积, 从而计算效率更高, 但是当输入向量的维度d比较高, 点积模型的值通常有比较大的方差, 从而导致softmax函数的梯度比较小，缩放点积模型可以较好 的解决此问题。双线性模型可以看作是一种泛化的点积模型, 假设双线性模型公式中 $W=U^{T} V,$ 原式可写为 $s\left(x_{i}, q\right)=x_{i}^{T} U^{T} V q=(U x)^{T}(V q),$ 分别对X和q进行线性
   变换后计算点积, 相比与点积模型, 双线性模型在计算相似度时引入了非对称性。
   加权平均：注意力分布 $\alpha_{i}$ 可以理解为在给定任务相关的查词q时，第i个输入向量受关注的程 度。 $a t t(X, q)=\sum_{i=1}^{N} \alpha_{i} x_{i}$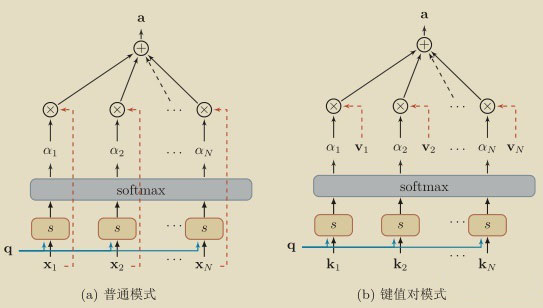
   

硬性注意力
软性注意力其选择的信息是所有输入信息在注意力分布下的期望。还有一种只关注到某一位置上的 信息，叫做硬性注意力(Hard Attention)。
选择最高概率的输入信息: $\quad a t t(X, q)=x_{j},$ j为概率最大的输入信息的下标，即

$$j=\operatorname{argmax} \alpha_{i}, i \in[1, N]$$

硬性注意力缺点是基于最大采样或随机采样的方式来选抨信息。因此最终的损失函数与注意力分布 之间的函数关系不可导，无法使用反向传播算法进行训练。为了使用反向传播算法，一般使用软性 注意力来代替硬性注意力。
键值对注意力
可以用键值对(key-value pair)格式来表示输入信息，其中 “键” 计算注意力分布 $\alpha_{i},$ “值”用来 计算聚合信息。
用 $(K, V)=\left[\left(k_{1}, v_{1}\right), \ldots,\left(k_{N}, v_{N}\right)\right]$ 表示N个输入信息，给定任务相关的查词向量q时, 注意力函数：

$$a t t((K, V), q)=\sum_{i=1}^{N} \alpha_{i} v_{i}=\sum_{i=1}^{N} \frac{\exp \left(s\left(k_{i}, q\right)\right)}{\sum_{j=1}^{N} \exp \left(s\left(k_{j}, q\right)\right)} v_{i}$$

其中 $s\left(k_{i}, q\right)$ 为打分函数.当 $K=V$ 时，鍵值对模式就等价于普通的注意力机制。