正则化的定义
首先,我们来简单认识一下什么是正则化。对于机器学习的算法,我们要尽可能的降低训练的错误率,而对于深度学习而言,只要给予足够多的神经元,理论上错误率可以达到无穷小,但是同时也会带来严重的问题,就是过拟合!因此,我们需要采取一些手段,去尽可能的降低验证错误率(有时需要牺牲训练的错误率),这种操作一般统称为正则化~
过拟合的本质就是由于算法模型能力过于强大,将数据中的一些不重要信息(例如噪声)也学习到模型之中,使模型的泛化性降低,从而使得验证集错误率升高,因此常见的正则化方法为限制学习算法能力,当然还有一些其他的手段作为辅助,下面我来一 一介绍~
参数范数惩罚
参数范数惩罚是最常见的正则化手段之一,其本质就是限制模型的能力,其中最著名的方法有L0、L1以及L2范数惩罚。
L0范数惩罚
最小化目标函数,并使得不等于0的参数个数控制在c个以下,以保证模型能力不至于过强。
L0范数惩罚限制算是比较苛刻的,而且函数不可导,因此实际应用时并不是十分友好。
L1范数惩罚
最小化目标函数,并使得参数数值的绝对值总和小于常数c,以限制魔性能力:
L1范数惩罚又称参数稀疏惩罚,相比于L0范数惩罚,其限制相对放宽了一些,虽然说函数仍然不可导,但是我们可以利用一些辅助函数代替微分。
L2范数惩罚
最小化目标函数,并使得参数的平方和小于常数c:
L2范数惩罚是最常用的范数惩罚,其限制相对宽松,函数可导,又称作权重衰减惩罚!
如图所示: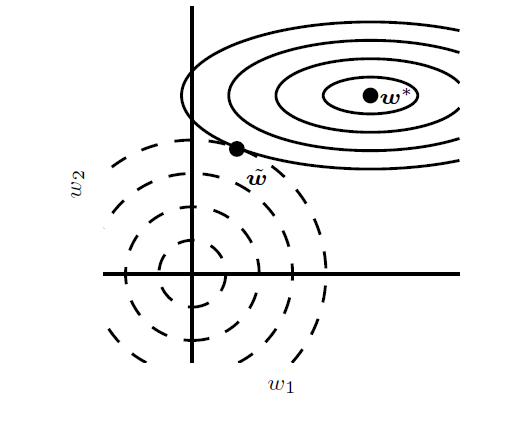
上图为L2参数正则化的模型图,代价函数的梯度如实线等高椭圆所示,如果没有任何限制,那么学习的过程就是沿着梯度等高线垂直的方向寻找极值,而图中的虚线如图所示,就是权重衰减项,虚线圆的半径就是权重衰减项中的常数c,两者的交点就是我们最后优化得到的最优值~
目标函数
L1范数
L2范数
范数惩罚小结
L0、L1、L2参数范数惩罚限制能力依次减弱,其限制算法能力通过限制参数实现的,也就是说令我们模型的参数更多的等于0,或者更多的接近于01,也就是我们常说的稀疏性。稀疏性最重要的一点就是有利于特征选择,由于大多数参数为0,或者说接近于0,从而这些参数对应的特征就没有被使用,实际上我们就选择了一些重要特征对数据进行预测,并自动筛选掉一些无用特征,这些无用特征很大程度上可能是噪声特征。
参数共享
在图像识别领域,图像应该具有平移、旋转等空间不变性特征;而对于时间序列数据为数据与数据之间应该具有时间不变性特征。例如,一幅图中有一只小猫,如果将该图中的每个像素都向右平移一个像素点,这只小猫依然在图中。对于人而言,平移一个像素点根本分辨不出区别,但对于机器学习算法而言,所有的像素特征对应的参数都发生了偏移,而机器学习算法很可能就认为这是两幅图像。为了提取到这种不变性特征,我们迫使相邻数据特征参数相同,而这种正则化方法也称为参数共享( Parameter Sharing)
卷积神经网络( Convolutional Neural Network,CN)的是目前最流行的一种神经网络广泛应用于计算机视觉领域。而该网络的核心一卷积操作,其实就是参数共享。参数共享使得卷积网络极大地降低了参数的规模,并且在不增加训练数据量的前提下,增加了网络的尺寸。
数据扩充与噪声注入
数据扩充
一般来说,想要降低泛化误差做好的方法就是训练更多的数据,但是现实中,数据量总是有限的,并且还需要大量成本,因此我们就想要人为的生成一些数据,也就是说“伪造数据”,然后将这些数据添加到训练集中进行数据扩充。但是能够进行数据扩充的任务并不是很多,最典型的就是对象识别,因为图片是一种高纬度复杂数据,具有平移,旋转不变性!我们对图片进行简单的平移,旋转、或者拉伸之后,就又是一个全新的数据了,但是,注意一点在对图片进行变换时,不能改变原有性质,例如在字符识别中,将‘b’进行镜像变换为‘d’,这样会生成错误数据,严重影响准确率!
噪声注入
在输入中注入噪声
数据扩充也可以看作是在输入数据中注入噪声,从而追使算法拥有更强的健壮性(也可以将注入噪声看作是一种数据扩充)。神经网络容易过拟合的原因之一就是对于噪声没有太好的抗噪能力。正所谓“你怕什么,就应该勇敢地去面对什么。”最简单的提高网络抗噪声能力方法,就是在训练时加入随机噪声一起训练。比如在非监督学习算法降噪自动编码器中,在输入层进行噪声注入然后学习无噪声的图片,便是一种很好的提高网络健壮性的方式。
在隐藏层注入噪声
对于某些模型,注入噪声也相当于对参数进行范数惩罚,通常而言,注入噪声要比简单地收缩参数更有效,尤其是将噪声注入到隐藏层中,该方法也可以看作是通过加入噪声重构新输入的一种正则化策略。
除了在数据以及隐藏层输入中注入噪声,在权重(参数)中注入噪声也是一种有效的正则化措施。这种方法在某种程度上可以等价地解释为传统的范数惩罚,该方法鼓励参数找到个参数空间,而该空间对于微小的参数变化所引起的输出变化的影响很小,换而言之,就是将模型送进了一个对于微小变化不敏感的区域,我们不仅找到了最小值,我们还找到了个宽扁的最小值区域
在类标中注入噪声
数据集中或多或少都带有错误的类标y,如果我们使用这些数据进行训练,那这就好比个专心听讲且对老师十分尊敬的好学生,认真学习老师教给他的所有知识,但老师教给他的却是错误的知识。最不幸的是,学生还对老师深信不疑,即使发现了错误,也只会认为是自己愚钝,不断地否定自己,不断地在痛苦中挣扎。虽然我们竭尽全力地避免错误标记数据但这并不如我们想象得那么美好,人为地添加错误在所难免。与其小心翼翼地标记数据做个完美的“老师”,还不如直接就告诉学生“老师”并不完美,“老师”也会犯错。而解决这种问题的具体措施就是在类标中加入一定的噪声,例如可以设置一个很小的常数c,我们将训练数据的类标y正确的概率设置为1-c。
稀疏表征
在上面的描述中,我们通过直接限制可用参数规模,如L1,L2参数范数惩罚,来限制模型的能力,从而降低过拟合风险。接下来,我们介绍一种通过作用在神经网络激活单元的惩罚策略,来提高隐藏层的稀疏性,该方法可算作是一种间接的模型参数惩罚。
生物进化的一个重要趋势就是尽可能地节约能源,而我们的大脑也符合节能的原则。大脑中每个神经元都连接着成千上万的神经元,但其实大部分神经元都是处于抑制状态,只有少部分的神经元接受刺激会处于激活状态,因此我们需要将特定的信息交给特定的神经元进行处理。受此启发,我们就期望使用某种惩罚措施来抑制大部分神经元。当信息输入进神经网络时,只有关键部分神经元才能够处于激活状态,这就是稀疏表征。
我们已经讨论过L1范数如何致使参数稀疏化,这就意味着大多数参数都为零或接近于零,而表征稀疏化描述的其实就是隐藏层的输出大多数为零或接近零。为了简明地阐述这些区别我们以一个线性回归为例,如下所示,第一个参数稀疏化的线性回归模型,第二个是使用稀疏表征的线性回归。
虽然表征正则化与参数正则化(一个使得输出稀疏,一个使得参数稀疏)有些区别,但幸运的是它们都使用相同的机理来实现。如下式所示,表征范数惩罚也是通过在代价函数中添加一项表征惩罚项$\Omega(h)$来实现表征稀疏化。
其中$\alpha$控制着惩罚项的惩罚力度,如果$\alpha=0$, 则相当于没有任何惩罚,$\alpha$越大,惩罚力度越大。
就如同在参数中使用L1惩罚,通过限制参数的总数值来诱使参数稀疏化一样,在表征征罚中我们也使用和L1 惩罚相同的方式:$\Omega(h)=||h|| $来诱使表征稀疏化。当然,L1征罚并不是唯一诱导稀疏表征的方法,其中KL散度, 又称相对摘也是一种十分常用的方法,有兴趣的读者可以自行查阅相关资料,这里就不再介绍。
早停
早停,简单来说就是在合适的时间选择停下,将训练次数作为一个超参数来寻找合适的值。目前,主流的方向有两种,第一种将训练集划分为真训练集与验证集,利用真训练集进行训练,利用验证集测试误差,找到最佳训练次数,最后利用所有的训练集训练,次数为上次的最佳迭代次数;第二种,同样将训练集划分为真训练集与验证集,利用真训练集进行训练,利用验证集测试误差,找到最佳训练次数,记录此时的训练误差,最后利用所有的训练集训练,直到训练误差小于等于之前的训练误差为止!
两种方法都有一定的局限性,第一种方法无法保证利用所有的数据得到的模型一定会优于第一步得到的模型;第二种方法无法保证模型的误差一定会小于最佳误差,从而导致无限循环迭代!
Dropout
个体与集成
集成学习通过构建并结合多个学习器来完成学习任务,换而言之,就是我们所谓的“套体主义”, 通常先训练一组个体学习器 , 然后再用某种策路将它们结合起来。个体学习器可以相同也可以不同,如果个体学习器相同,集成就标为是同质的, 同质集成的个体学习器就称为基学习器 , 如神经网络就是典型的神经元集成起来的;如果个体学习器不相同,那我们的集成就称为是异质的, 异质集成的个体学习器由不同的学习算法生成,而此时的个体学习器就不被称为基学习器,而称为组件学习器。
其实同质集成与神经网络在最终结构上是一样的,之所以把神经网络和集成学习分开来看待,是其组织方式的不同。集成学习是一种"自底向上”的构建方式,我们先要获得学习器,然后再关注如何将其组织起来形成一个整体。而神经网络通常是一种“自顶向下”的构建方式,我们先将各学习器构建起来,再关注如何学习调整结构内的每个学习器。
集成学习最重要的核心思想在于:集体比个体好。那集体凭什么就比个体好呢?要回答这个问题,我们需要再次谈谈机器学习的两个核心问题,欠拟合与过拟合问题。对应到集成学习领域也有两个主要的应对措施,那就是 Bagging 思想与 Boosting 思想。欠拟合是因为模型能力不足引起的,再说得直观些就是我们的学习器只能学习到数据处一部分特征,这些特征不足以解释所有的数据特性。那如何解决呢?比如进行人脸识别任务,但我们训练的学习器的能力有限,只能识别局部特征,比如只能识别鼻子。那很简单,我们让接下来的学习器识别耳朵,再让下一个学习器识别眼睛,那这样集成出来的学习器就可以很好地识别人脸了。这种“弱弱联合"变强的方式在集成学习中就称为Boosting。
同样地,过拟合问题是因为模型能力太强所致,更直观些就是我们的学习器不仅能学习到数据的特征,还能学习到数据的噪声特征。这些特征足以解释所有的训练数据,但却严重影响了测试数据。就比如我们进行人脸识别,学习器不仅学习到眼睛、鼻子、耳朵等人脸特征,还学习到了训练数据中人的衣服、发型、甚至是雀斑等无用特征。虽然训练结果很好,但在测试数据中却不一定有这些特征,那测试结果必然糟糕。那我们如何使用集成方式去制约这种连“人脸雀斑”都能学习到的能力呢?那也很简单,比如第一个学习器除了学习拟脸特征外还能学习到“衣服特征”, 下一个学习器还能学习除了人脸特征之外的“发型特任”,再下一个学习器还能学习“雀斑特征”。我们将这些学习器组合起来形成“强强制约”的情况,这就是集成学习中的Bagging的思想
不论是“弱弱联合”的 Boosting, 还是“强强制约”的Bagging 都有一个核心,那就是应该尽可能的多样。这里所说的“多样性”, 不仅指集成学习器的数量越多越好,更重要的是学习器之间应该尽可能的“不同”, 学习器的不同其实就是学习到数据特征的不同。如果学习器相似,那么获取到的特征也就相似,“弱弱联合”依然只是“臭皮匠”的愚盘,“强强组合”也只是加固其“书呆子”的偏执。
如何才能获取学习器的多样性呢?其实只有一个方式,那就是数据。从行为心理学的观出发,所有人的思想行为都是一样的,人与人之所以看似不同,其实是接触到的生长环境不同造成的。当然,这种观点对于解释人而言肯定是不足的,但对于解释机器学习却很友好。如果我们使用相同的数据,相同的学习算法,那我们得到的学习器也就基本相同。对于同质集成,如果我们想要获取不同的学习器,那我们就应该给予其不同的数据进行训练。
对于 Bagging 而言,想要获取多样性的学习器,我们就通过从训练数据中随机采样一定的子数据集进行训练。训练得到学习器后,再将数据放回原始训练集中进行下一次随机采样来训练下一个学习器。如此重复进行,直到学习器的数目达到预设数量为止,这种方法也叫自助采样法。这种方法的关键点在于采样率的选择,如果采样率过高,采样数据集的相似性也就过高,学习器的“不同”就很难保证:如果采样率过低,那训练数据不足,个体学习器的性能就较差。在实践经验中,常采用 63. 2%的采样率,但这并不是一条铁律,最佳的采样率还需要根据具体数据,具体问题进行实验。
对于Boosting 而言,我们首先会使用所有训练数据去训练第一个学习器,但该学习器只会对某些数据识别较好,对于另一些数据识别较差(如果都好,就是强分类器了,不需要集成了)。接下来我们就使用下一个学习器,着重地学习前一个学习器识别较差的数据,而忽略之前识别较好的数据。如此重复进行,当学习器的数目达到预设数量后停止学习。
总之,依靠“好而不同”的个体,我们可以得到强而有力的集体。有了对集成学习最粗浅的认识后,接下来就开始介绍本节的主角-Dropout.
Dropout
如何将集成学习与神经网络结合起来呢?一个很自然的想法就是将神经网络当作基学习器(个体学习器)来训练,然后再将每个神经网络集成起来,这种方法最大的问题在于需要极大的训练时间及足够的内存消耗。神经网络最让人闻风丧胆的地方就是其可怕的训练时间,然后我们还想在此基础上训练多个神经网络,想想就可怕。当然,这确实也是一种好方法。如要条件允许,集成5到10个神经网络,其效果还是非常好的。
有没有又可以集成多个神经网络,又可以节约训练时间的方法呢?在上文中,我们将神经网络当作基学习器来看待,而现在我们需要换一个角度,我们将神经网络当作最终集成起来的结果进行思考。但又不太一样,你可能很容易会想到,我们会将神经元当作个体学习器进行学习。但如果那样,我们其实又回到传统的同质集成循环中去了。如下图所示,神经网络可以分解成16种不同的子网络,而Dropout 所做的就是将神经网络中的弱子神经网络集成起来。
在 Bagging 的思想中,我们想要获得不同的学习器,需要从训练数据中采样出不同的训练集。然后通过训练数据集的不同,从而期望获得不同“观点”的学习器。那么 Dropout 如何构造不同的弱神经网络进行训练呢?
其实非常简单,我们会在训练阶段给每个神经元独立地设置一个二项分布的“神经元激活”概率,若该值为0, 则表明当前神经元抑制;如果该值为1, 则表明当前神经元可用。如下图所示,为激活概率是0. 5时,Dropout 所构造出弱神经网络的结构,该弱神经网络的神经元数量及参数数目(连接权重数量)都被极大地限制了。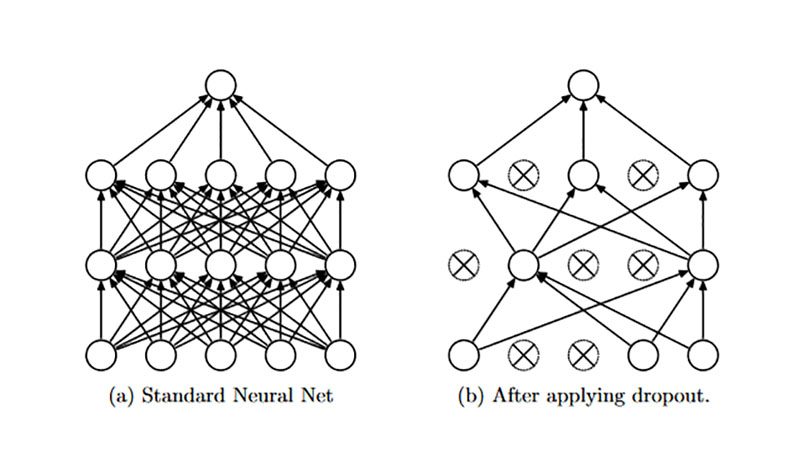
Dropout分为训练阶段与测试阶段,训练阶段相比于传统的前馈神经网络,只是多了一个神经元采样过程,而训练则采取随机梯度下降或最小批量梯度下降的方式进行。其实就是随机激活一定数量的神经元,然后执行一条或一小批数据,对激活的神经元进行误差反向传播修正权重,然后再次随机激活神经元训练网络。在测试或执行阶段,将神经元采样过程移除,退化为传统的神经网络进行测试。
Dropout 可以看作是集成学习中 Bagging 的一种形式,通过神经元采样构造不同的网络结构,然后通过采样出不同的数据来训练不同的弱神经网络。但这其中和 Bagging 还有个非常不一样的地方,那就是神经元共享。
神经网络中的每个隐藏单元经过 Dropout 训练后,它必须学习与不同采样的神经元间的合作,这使得神经元具有更强的健壮性,并且驱使神经元通过自身获取到有用特征,而不是依赖其他神经元去纠正自身的错误。在Dropout中,我们引入了一个神经元采样概率p 超参数,在默认情况下该值设置为0. 5, 但这不是一个定量,根据数据和网络的不同,还需要在试验中反复地测试。

